Home Page

Info

I’m a data scientist, with a M.Sc. in Robotics and Ph.D. in Machine Learning domains obtained at the Technion - Israel Institute of Technology. Prior to the M.Sc., I had a long history of working in the software development industry, both as a R&D engineer and as a team leader.

My current research interests lay within different theoretical and practical aspects of probabilistic model learning, kernel methods and non-convex optimization theory.

$\newcommand{\RR}{\mathbb{R}}$ $\newcommand{\usuff}{\scriptscriptstyle U}$ $\newcommand{\dsuff}{\scriptscriptstyle D}$ $\newcommand{\probi}[2]{\mathbb{P}^{#1}({#2})}$ $\newcommand{\udata}{\{X_i^{\usuff}\}_{i = 1}^{N^{\usuff}}}$ $\newcommand{\ddata}{\{X_i^{\dsuff}\}_{i = 1}^{N^{\dsuff}}}$

General Probabilistic Surface Optimization

I graduated with my Ph.D. in probabilistic model estimation, with a dissertation titled “General Probabilistic Surface Optimization”. This work focuses on probabilistic estimation tasks based on energy contrast equilibrium, providing a framework for constructing an infinite number of objective functions to learn various valuable probabilistic target functions (e.g. probability density of data). It can be further viewed as a generalization of many existing statistical objective functions such as cross entropy and noise contrastive estimation, and provides an intuitive geometrical perspective on a typical optimization task.

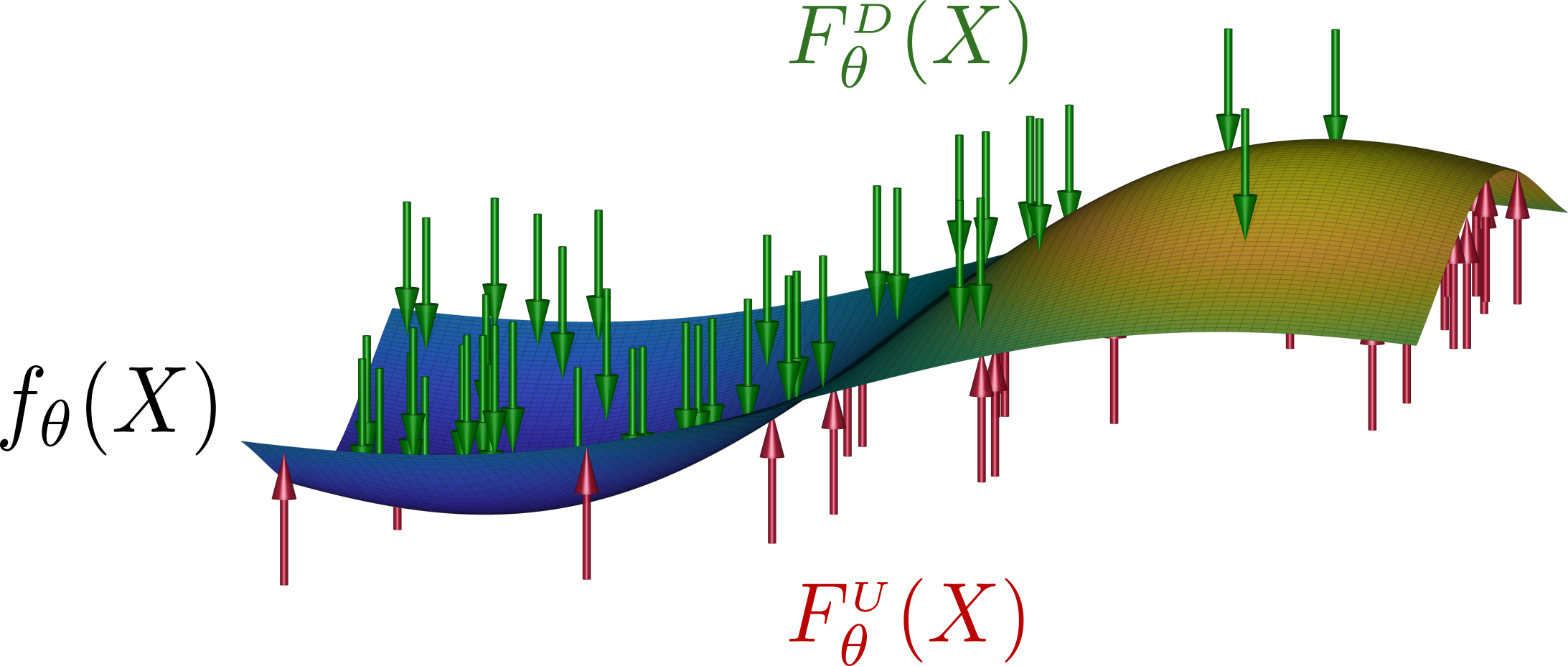
Illustration of PSO principles: model $f_{\theta}(X): \RR^{n} \rightarrow \mathbb{R}$ (e.g. a neural network, NN, parametrized by $\theta$ or a kernel model) represents a virtual surface that is pushed in opposite directions - up at points $\udata$ sampled from density $\probi{\usuff}{X}$ and down at points $\ddata$ sampled from density $\probi{\dsuff}{X}$. Magnitude of each push is amplified by analytical function - $M^{\usuff}\left[X,f_{\theta}(X)\right]$ when pushing at $X_i^{\usuff}$ and $M^{\dsuff}\left[X,f_{\theta}(X)\right]$ when pushing at $X_i^{\dsuff}$, where both functions may have an almost arbitrary form, with only minor restrictions. During an iterative optimization $\theta_{t+1} = \theta_{t} - \delta \cdot d\theta$ via PSO loss gradient:

$d\theta = - \frac{1}{N^{\usuff}} \sum_{i = 1}^{N^{\usuff}} M^{\usuff} \left[ X^{\usuff}_{i}, f_{\theta}(X^{\usuff}_{i}) \right] \cdot \nabla_{\theta} f_{\theta}(X^{\usuff}_{i}) + \frac{1}{N^{\dsuff}} \sum_{i = 1}^{N^{\dsuff}} M^{\dsuff} \left[ X^{\dsuff}_{i}, f_{\theta}(X^{\dsuff}_{i}) \right] \cdot \nabla_{\theta} f_{\theta}(X^{\dsuff}_{i})$ ,

the up and down pointwise forces $F_{\theta}^{\usuff}(X) = \probi{\usuff}{X} \cdot M^{\usuff}\left[X,f_{\theta}(X)\right]$ and $F_{\theta}^{\dsuff}(X) = \probi{\dsuff}{X} \cdot M^{\dsuff}\left[X,f_{\theta}(X)\right]$, containing both frequency and analytical components, adapt to each other till the point-wise balance state $F_{\theta}^{\usuff}(X) = F_{\theta}^{\dsuff}(X)$ is achieved.

Such convergence causes the final model $f_{\theta}(X)$ to be a specific function of $\probi{\usuff}{X}$ and $\probi{\dsuff}{X}$, by satisfying PSO balance state:

$ \frac{\probi{\usuff}{X}}{\probi{\dsuff}{X}} = \frac{M^{\dsuff}\left[X,f_{\theta}(X)\right]}{M^{\usuff}\left[X,f_{\theta}(X)\right]} $ ,

and it can be used for inferring numerous statistical functions of arbitrary data. Particularly, PSO delivers exact tools to control magnitude functions $M^{\usuff}$ and $M^{\dsuff}$ for approximation of any desired $T\left[X, \frac{\probi{\usuff}{X}}{\probi{\dsuff}{X}} \right]$ from datasets {$X_i^{\usuff}$}_$i$ and {$X_i^{\dsuff}$}_$i$ (see Sections 3 and 5 of thesis for more details).

Dynamics of Neural Tangent Kernel

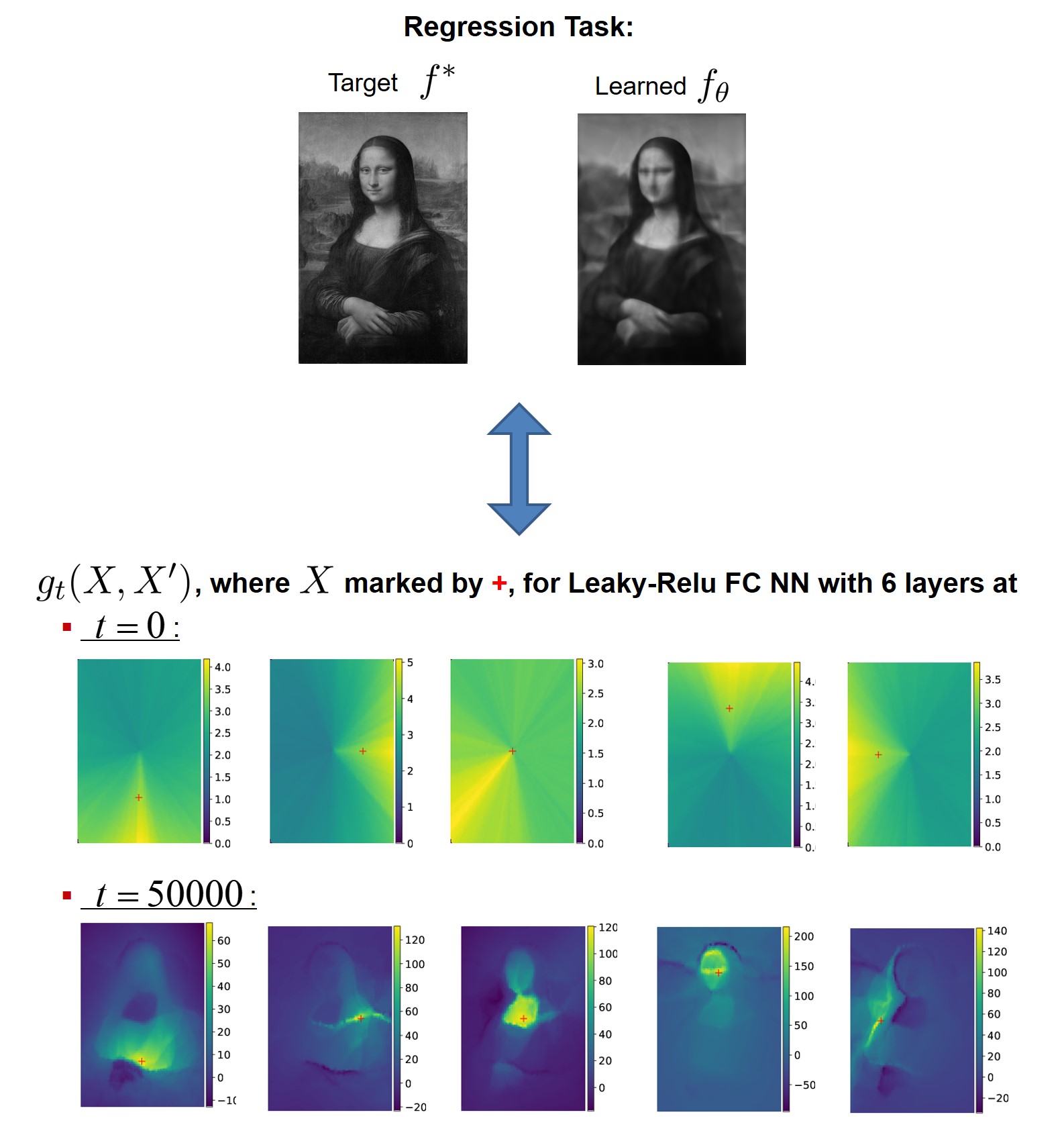
A typical gradient-based optimization may be viewed as pushing over a flexible surface (PSO is built on this idea exactly). The impact of pushing at any particular point $X$ can be described via the model kernel $g_{\theta}(X, X’) \triangleq \nabla_{\theta} f_{\theta}(X)^T \cdot \nabla_{\theta} f_{\theta}(X’)$. This kernel is responsible for interpolation and extrapolation during the optimization process, also defining what functions are easier to learn and what will be the generalization performance. Additionally, it can be intuitively considered as a description of the pushing “wand” we use when pushing $f_{\theta}$ at $X$.

In case we use kernel models, $g_{\theta}(X, X’)$ is identical to the reproducing kernel and is constant during the entire optimization process. If we use NNs, this kernel is known as Neural Tangent Kernel (NTK) [Jacot et al., 2018], and is time-variant. My study of NTK and its dynamics during NN learning process emphasizes the importance of the model kernel adaptation to the specific target function for a good learning outcome (see Section 14 of thesis for more details).

Files

Thesis - the final dissertation file.

Presentation - a (relatively) short description of PSO and model kernel dynamics, to get a grasp over unsupervised learning domain in a quick and intuitive manner.